Sistema de ecuaciones

Un sistema de ecuaciones es un conjunto de dos o más ecuaciones con varias
incógnitas que conforman un problema matemático consistente en encontrar las
incógnitas que satisfacen dichas ecuaciones.
En un sistema de ecuaciones algebraicas las incógnitas son valores numéricos
(o más generalmente elementos de un cuerpo sobre el que se plantean las
ecuaciones), mientras que en una ecuación diferencial las incógnitas son funciones
o distribuciones de un cierto conjunto definido de antemano. 
Una solución de dicho sistema es por tanto, un valor o una función que substituida
en las ecuaciones del sistema hace que éstas se cumplan automáticamente sin
que se llegue a una contradicción. En otras palabras el valor que reemplazamos
en las incógnitas debe hacer cumplir la igualdad del sistema.
Las incógnitas se suelen representar utilizando las últimas letras del alfabeto latino
o si son demasiadas, con negras subíndices.
La forma genérica de un sistema de ecuaciones algebraicas y incógnitas es
la siguiente:

donde 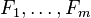son funciones de las incógnitas. La solución, perteneciente
al espacio euclídeo , será tal que el resultado de evaluar cualquier expresión
con los valores de dicha solución, verifique la ecuación.