MATRIZ

En matemáticas, una matriz es una tabla bidimensional de números consistente
en cantidades abstractas que pueden sumarse y multiplicarse. Las matrices se
utilizan para describir sistemas de ecuaciones lineales, realizar un seguimiento
de los coeficientes de una aplicación lineal y registrar los datos que dependen
de varios parámetros.

Ejemplo

Dada la matriz:

que es una matriz 4x3. El elemento o es el 7.
La matriz

es una matriz 1×9, o un vector fila con 9 elementos.

Suma o adición

Dadas las matrices m-por-n ,A y B, su suma A + B es la matriz m-por-n
calculada sumando los elementos correspondientes
(i.e. (A + B)[i, j] = A[i, j] + B[i, j] ). Es decir, sumar cada uno de los
elementos homólogos de las matrices a sumar. Por ejemplo:

Propiedades

• Asociativa

Dadas las matrices m×n A, B y C

(A + B) + C = A + (B + C)

• Conmutativa

Dadas las matrices m×n A y B

A + B = B + A

• Existencia de matriz cero o matriz nula

A + 0 = 0 + A = A

• Existencia de matriz opuesta

con gr-A = [-a_ij]

A + (-A) = 0

(C-I2)-1(AT+B)

Producto por un escalar

Dada una matriz A y un escalar c, su producto cA se calcula multiplicando
el escalar por cada elemento de A (i.e. (cA)[i, j] = cA[i, j] ).

Ejemplo

RESOLUCIÓN DE UN SISTEMA DE ECUACIONES POR EL MÉTODO DE ELIMINACION

Para resolver por eliminación un sistema de ecuaciones 2×2 el procedimiento que 

se sigue es el ilustrado con el ejemplo presentado a continuación:

Resuélvase el siguiente sistema de ecuaciones

1. 2x + 4y = 20

2. 3x + y = 10

1. Se multiplican los coeficientes de las variables de una o ambas ecuaciones de

ser necesario, buscando obtener el valor negativo de una de las variables de una

ecuación en la otra.

2x + 4y = 20

.

3x + y = 10 (−4)

Multiplicamos la ecuación 2 por (−4) para obtener – 4y. El resultado sería:

2x + 4y = 20

.

-12x - 4y = −40 Ecuación resultante

2. Restamos la ecuación resultante de multiplicar la 2 por (−4) de la ecuación 1

para dejar una ecuación en términos de una sola variable. Obteniendo:

2x + 4y = 20

-12x - 4y = −40

-10x = −20

3. Despejamos la variable restante para obtener su valor.

En este caso la variable despejada es x, quedando:

x= −20/−10

x= 2

4. El resultado obtenido se sustituye en cualquiera de las ecuaciones originales

para obtener el valor de la variable restante. En este caso tomamos la ecuación 1

quedando como sigue:

2x + 4y = 20, sí x= 2 entonces y será

2(2) + 4y = 20

4 + 4y = 20

4y = 20 – 4

4y = 16

y=16/4

y= 4

Siendo los valores que satisfacen mi sistema de ecuaciones de x= 2, y=4.

RESOLUCIÓN DE UN SISTEMA DE ECUACIONES POR EL MÉTODO DE SUSTITUCIÓN

Sea el sistema
Primero en una de las ecuaciones se halla el valor de una de las incógnitas. Hallemos la y en la primera ecuación supuesto conocido el valor de x

y=11-3x

Se sustituye en la otra ecuación el valor anteriormente hallado

5x-(11-3x)=13

Ahora tenemos una ecuación con una sóla incógnita; la resolvemos

5x-11+3y=13

5x+3x=13+11

8x=24

x=3

Ya conocido el valor de x lo sustituimos en la expresión del valor de y que obtuvimos a partir de la primera ecuación del sistema

y=11-3x

y=11-9

y=2

Así la solución al sistema de ecuaciones propuesto será x=3 e y=2

Resolución y representación gráfica de sistemas de ecuaciones lineales

Resolvemos gráficamente el sistema x + y = 6; x - y = 2}

1. ^o Despejamos y en las dos ecuaciones.
   x + y = 6 → y = 6 - x
   x - y = 2 → y = x - 2
2. ^o Dando valores a x, formamos una tabla de valores para cada una de las dos ecuaciones.

y = 6 - x

x	0	1	2	3	4
y	6	5	4	3	2

y = x - 2

x	0	1	2	3	4
y	-2	-1	0	1	2

1. ^o Representamos estos puntos sobre un sistema de ejes.

 

Uniendo los puntos de cada ecuación, obtenemos dos rectas que representan todas las 

soluciones de cada una de las ecuaciones

1. ^o Puede ocurrir uno de los siguientes casos:
   • Si las rectas no se cortan, es decir, son paralelas, el sistema es incompatible no tiene solución.
   • Si las rectas se cortan en un punto, el sistema tiene solución única. Decimos que es compatible determinado.
   • Si las dos rectas coinciden, esto es, son la misma, el sistema tiene infinitas soluciones. Es un sistema compatible indeterminado.
   En nuestro caso, las rectas se cortan en el punto (4, 2). La solución del sistema es x = 4 e y = 2.

Sistema de ecuaciones

Un sistema de ecuaciones es un conjunto de dos o más ecuaciones con varias
incógnitas que conforman un problema matemático consistente en encontrar las
incógnitas que satisfacen dichas ecuaciones.
En un sistema de ecuaciones algebraicas las incógnitas son valores numéricos
(o más generalmente elementos de un cuerpo sobre el que se plantean las
ecuaciones), mientras que en una ecuación diferencial las incógnitas son funciones
o distribuciones de un cierto conjunto definido de antemano. 
Una solución de dicho sistema es por tanto, un valor o una función que substituida
en las ecuaciones del sistema hace que éstas se cumplan automáticamente sin
que se llegue a una contradicción. En otras palabras el valor que reemplazamos
en las incógnitas debe hacer cumplir la igualdad del sistema.
Las incógnitas se suelen representar utilizando las últimas letras del alfabeto latino
o si son demasiadas, con negras subíndices.
La forma genérica de un sistema de ecuaciones algebraicas y incógnitas es
la siguiente:

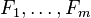donde son funciones de las incógnitas. La solución, perteneciente
al espacio euclídeo , será tal que el resultado de evaluar cualquier expresión
con los valores de dicha solución, verifique la ecuación.