En el ámbito de la
estadística, la mediana, representa el valor de la variable de posición central en un conjunto de datos ordenados. De acuerdo con esta definición el conjunto de datos menores o iguales
que la mediana representarán el 50% de los datos, y los que sean mayores que la mediana
representarán el otro 50% del total de datos de la muestra. La mediana coincide con el
percentil 50, con el segundo cuartil y con el quinto decil
Existen dos métodos para el cálculo de la mediana:
- Considerando los datos en forma individual, sin agruparlos.
- Utilizando los datos agrupados en intervalos de clase.
A continuación veamos cada una de ellas
Datos sin agrupar
Sean

los datos de una muestra
ordenada en orden creciente y designando la mediana como
Me, distinguimos dos casos:
a) Si
n es impar, la mediana es el valor que ocupa la posición
(n + 1) / 2 una vez que los datos han sido ordenados (en orden creciente o decreciente), porque éste es el valor central. Es decir:
Me = x(n + 1) / 2.
Por ejemplo, si tenemos 5 datos, que ordenados son:
x1 = 3,
x2 = 6,
x3 = 7,
x4 = 8,
x5 = 9 => El valor central es el tercero:
x(5 + 1) / 2 = x3 = 7. Este valor, que es la mediana de ese conjunto de datos, deja dos datos por debajo (
x1,
x2) y otros dos por encima de él (
x4,
x5).
b) Si
n es par, la mediana es la media aritmética de las dos observaciones centrales. Cuando
n es par, los dos datos que están en el centro de la muestra ocupan las posiciones
n / 2 y
n / 2 + 1. Es decir:
Me = (xn / 2 + (xn / 2 + 1)) / 2.
Por ejemplo, si tenemos 6 datos, que ordenados son:
x1 = 3,
x2 = 6,
x3 = 7,
x4 = 8,
x5 = 9,
x6 = 10 =>
Hay dos valores que están por debajo del
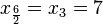
y otros dos que quedan por encima
del siguiente dato

. Por tanto, la mediana de este grupo de datos es la media
aritmética de estos dos datos:
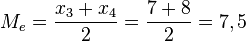
.
Datos agrupados
Al tratar con datos agrupados, si

coincide con el valor de una frecuencia acumulada,
el valor de
la mediana coincidirá con la abscisa correspondiente. Si no coincide con
el valor de ninguna abcisa, se calcula a través de semejanza de triángulos
en el histograma o polígono de frecuencias acumuladas, utilizando la siguiente equivalencia:

Dónde
Ni y
Ni − 1 son las frecuencias absolutas acumuladas tales que

,
ai − 1 y
ai son los extremos, inferior y superior, del intervalo
donde se alcanza la mediana y
Me = ai − 1 es la abscisa a calcular, la moda.
Se observa que
ai − ai − 1 es la amplitud de los intervalos seleccionados para el diagrama.
.














 los datos de una muestra ordenada en orden creciente y designando la mediana como
los datos de una muestra ordenada en orden creciente y designando la mediana como 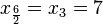 y otros dos que quedan por encima
y otros dos que quedan por encima  . Por tanto, la mediana de este grupo de datos es la media
. Por tanto, la mediana de este grupo de datos es la media 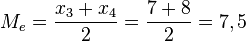 .
. coincide con el valor de una frecuencia acumulada,
coincide con el valor de una frecuencia acumulada,  ,
,  , la media aritmética se define simplemente como:
, la media aritmética se define simplemente como:

 ), mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
), mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.![\sqrt[n]{x_1 x_2 \dots x_n} \le \frac{x_1+ \dots + x_n}{n}](http://upload.wikimedia.org/wikipedia/es/math/8/e/6/8e601c29ce3964e378346560bff6a281.png)
